In een tijd waarin het internet vol staat met quizzen en hersenkrakers, heeft één ogenschijnlijk simpele rekensom miljoenen mensen aan het twijfelen gebracht: 8 ÷ 2(2 + 2).
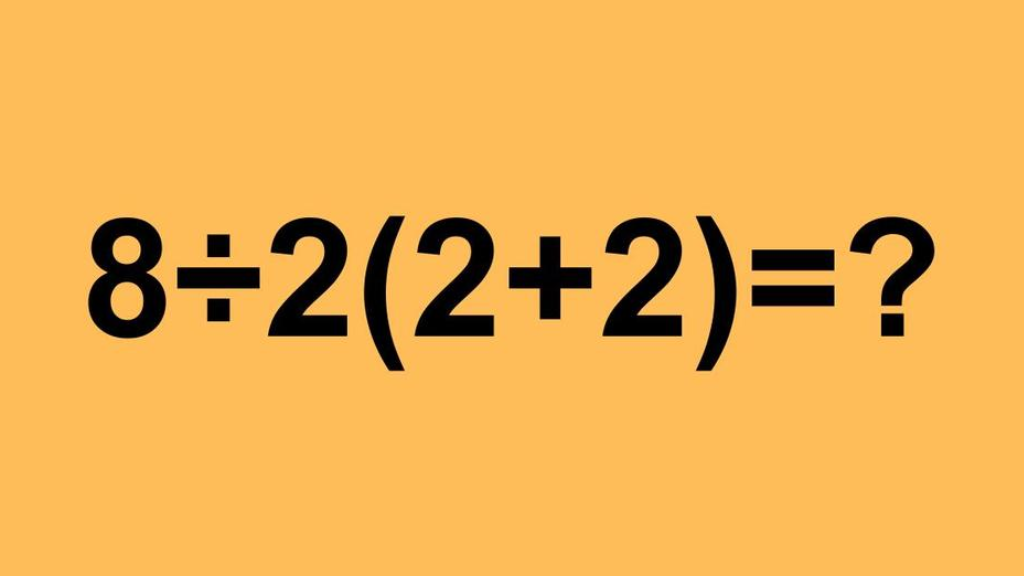 Wat op het eerste gezicht een basisschoolvraag lijkt, blijkt bij nadere beschouwing een bron van verwarring, frustratie en felle discussies te zijn — zelfs onder ervaren wiskundigen. Maar hoe kan zo’n simpele som zo veel opschudding veroorzaken?
Wat op het eerste gezicht een basisschoolvraag lijkt, blijkt bij nadere beschouwing een bron van verwarring, frustratie en felle discussies te zijn — zelfs onder ervaren wiskundigen. Maar hoe kan zo’n simpele som zo veel opschudding veroorzaken?
Waar komt deze discussie vandaan?
De oorspronkelijke post die de discussie deed oplaaien, verscheen in 2019 op Twitter en Reddit. In de post stond de wiskundige uitdrukking:
8 ÷ 2(2 + 2)
En de vraag: Wat is het juiste antwoord?
De reacties stroomden binnen en het viel al snel op dat mensen in twee kampen waren verdeeld: sommigen kwamen uit op 1, anderen zwoeren dat het 16 moest zijn. Beide groepen claimden de juiste aanpak te hebben gevolgd — wat leidde tot de hamvraag: wat is nou de correcte manier om deze som op te lossen?
De kern van het probleem: volgorde van bewerkingen
Om deze som op te lossen, moeten we de volgorde van bewerkingen begrijpen. De meeste mensen leren op school een ezelsbruggetje zoals “Haakjes, Exponenten, Vermenigvuldigen/Delen, Optellen/Aftrekken” — in het Engels bekend als PEMDAS of in het Nederlands vaak als “HVMOA”:
Haakjes > Vermenigvuldigen en Delen (van links naar rechts) > Optellen en Aftrekken (van links naar rechts)
Dit betekent dat bewerkingen binnen haakjes als eerste worden uitgevoerd. Daarna volgen vermenigvuldiging en deling, die gelijkwaardig zijn en dus van links naar rechts moeten worden afgewerkt. Tot slot komen optellen en aftrekken.
Oplossing stap voor stap: de weg naar 16
Laten we de som oplossen volgens deze standaardregels.
Start met de haakjes:
8 ÷ 2(2 + 2) → 8 ÷ 2(4)Vermenigvuldiging door juxtapositie (zonder teken):
2(4) betekent 2 × 4
Dus: 8 ÷ 2 × 4Van links naar rechts bewerken:
Eerst 8 ÷ 2 = 4
Daarna 4 × 4 = 16
Antwoord: 16
Volgens deze logische aanpak, die in moderne wiskundeboeken en rekenmachines wordt toegepast, is 16 het juiste antwoord. Maar waarom denken anderen dan dat het 1 moet zijn?
Het argument voor 1: prioriteit van vermenigvuldiging?
Sommige mensen lezen de uitdrukking anders:
8 ÷ 2(4) wordt gezien als 8 ÷ [2 × 4]
Als je dat zo interpreteert, reken je eerst 2 × 4 = 8, en vervolgens 8 ÷ 8 = 1
Dit is een klassieke misvatting, gebaseerd op het idee dat vermenigvuldiging vóór deling zou moeten komen. Maar dit klopt niet. Volgens de regels van de rekenvolgorde hebben vermenigvuldigen en delen dezelfde prioriteit, en moet je deze van links naar rechts uitvoeren.
Waarom is dit belangrijk?
Het misverstand toont iets fundamenteels aan over wiskundige communicatie. Hoewel de regels helder zijn, kunnen symbolen dubbelzinnig worden geïnterpreteerd, vooral als de notatie niet strikt is.
In sommige gevallen gebruiken wiskundigen explicieter gebruik van breuken of haakjes om verwarring te voorkomen, zoals:
(8 ÷ 2)(4) → geeft als resultaat 16
8 ÷ (2 × 4) → geeft als resultaat 1
Beide zijn wiskundig correct, afhankelijk van hoe de formule is geschreven. Maar 8 ÷ 2(4) is minder duidelijk, en dat veroorzaakt de twist.
De rol van rekenmachines en software
Zelfs rekenmachines zijn niet altijd het eens. Oudere modellen of software die niet volgens de moderne PEMDAS-regels werkt, kunnen andere antwoorden geven. Bijvoorbeeld:
Sommige eenvoudige rekenmachines interpreteren 8 ÷ 2(4) als 8 ÷ (2 × 4) = 1
Moderne grafische rekenmachines geven 8 ÷ 2 × 4 = 16
Programmeerplatforms zoals Python of Excel volgen strikte links-naar-rechtslogica voor deling en vermenigvuldiging, en komen dus uit op 16.
Wat kunnen we hiervan leren?
Wiskunde draait niet alleen om regels, maar ook om heldere notatie.
Slecht geschreven formules leiden tot meerdere interpretaties.Links-naar-rechts werkt alleen als je de volgorde van operaties begrijpt.
Vermenigvuldigen vóór delen is een misverstand; ze zijn gelijkwaardig in prioriteit.Bij twijfel: gebruik extra haakjes.
Daarmee geef je exact aan welke bewerkingen je bedoelt, en voorkom je misverstanden.
Waarom blijft dit vraagstuk populair?
De som is simpel genoeg om iedereen te betrekken, maar complex genoeg om verwarring te zaaien. Het laat ook zien hoe belangrijk het is om de regels van bewerkingen echt goed te begrijpen, en hoe zelfs ervaren mensen in de war kunnen raken bij vage notatie.
Wat is dan nu het juiste antwoord op 8 ÷ 2(2 + 2)?
Antwoord: 16
Volgens de geldende wiskundige conventies los je de haakjes op, en werk je vervolgens de deling en vermenigvuldiging van links naar rechts af. Zo kom je uit op 16 — en dat is het antwoord dat ook door de meeste professionele bronnen wordt bevestigd.
Het probleem draait om de volgorde van bewerkingen, waarbij sommigen vasthouden aan de conventionele wiskunderegels van ‘Haakjes wegwerken, machten en wortels uitwerken, vermenigvuldigen en delen, optellen en aftrekken’. Dit betekent dat volgens deze regel eerst de haakjes moeten worden opgelost, wat resulteert in 8 ÷ 2 x 4. Vervolgens moet de vergelijking van links naar rechts worden opgelost, waarbij deling vóór vermenigvuldiging gaat.
Volgens deze benadering komt het antwoord uit op 16, aangezien 8 gedeeld door 2 gelijk is aan 4, en vervolgens 4 vermenigvuldigd met 4. Deze interpretatie wordt ondersteund door veel traditionele wiskundigen en educatieve bronnen.
Aan de andere kant zijn er tegenstanders die beweren dat vermenigvuldiging voorrang moet hebben op deling, wat zou leiden tot een ander resultaat. Dit standpunt heeft ook aanhangers, waaronder wetenschappers die pleiten voor strikte naleving van de volgorde van bewerkingen volgens wiskundige conventies.
Deze discussie onderstreept niet alleen de complexiteit van wiskundige principes, maar ook hoe interpretatie en toepassing van regels kunnen leiden tot uiteenlopende uitkomsten.
Het wiskundeprobleem blijft een boeiend voorbeeld van hoe zelfs schijnbaar eenvoudige vraagstukken kunnen leiden tot diepgaande analyses en debatten binnen zowel academische kringen als online gemeenschappen.






