Dit lijkt misschien een simpele som. Een beetje rekenen, en klaar ben je. Toch is dit precies het soort raadsel dat discussies uitlokt en mensen in twee kampen verdeelt. Het gaat om de som: 6 ÷ 2 (1 + 2) = ?. Hoe moeilijk kan het zijn, denk je? Maar wacht even, want de uitkomst is niet zo vanzelfsprekend als je misschien denkt.
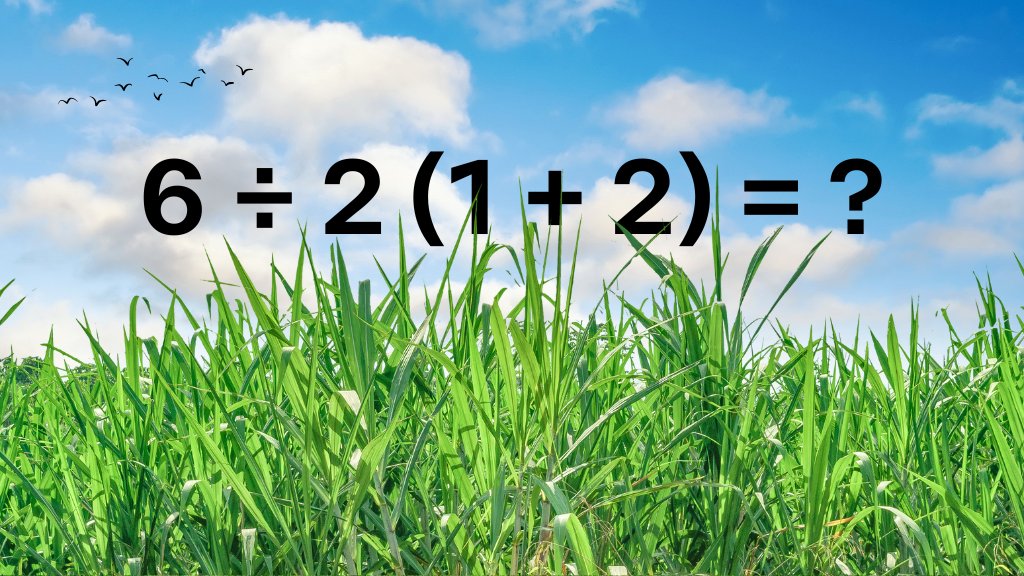
Iedereen die deze puzzel ziet, heeft meteen een antwoord in zijn hoofd. De één zegt 1, terwijl de ander vol overtuiging 9 roept. Hoe kan dat? Het gaat hier niet alleen om rekenen, maar vooral om de volgorde waarin je de bewerkingen uitvoert. En dat is precies waar veel mensen de mist in gaan.
Neem Tim, 28 jaar. Hij zag deze som voorbijkomen op social media en dacht dat hij het antwoord direct wist. “Ik deed het gewoon in mijn hoofd,” vertelt hij. “Eerst de haakjes, dan de rest. Mijn antwoord was 1. Maar toen ik in de reacties keek, waren mensen aan het zeggen dat het 9 was.
Ik snapte er niks meer van!” Hij besloot zijn rekenmachine erbij te pakken, maar zelfs die gaf hem een ander antwoord dan hij verwachtte. “Het voelde echt alsof ik iets miste.”
Het probleem zit in hoe je de volgorde van de bewerkingen interpreteert. Er bestaat een bekende regel in de wiskunde die hier van toepassing is: BODMAS of PEMDAS.
Het betekent dat je eerst de haakjes oplost, dan eventuele machten, gevolgd door delen en vermenigvuldigen, en tot slot optellen en aftrekken. Klinkt simpel, toch? Maar de manier waarop je die regels toepast, maakt een wereld van verschil.
Laten we eens kijken naar hoe dit fout kan gaan. Sommige mensen lezen de som als 6 ÷ (2 x (1 + 2)). Ze lossen eerst de haakjes op, wat 3 geeft. Daarna doen ze 2 x 3 = 6. Vervolgens delen ze 6 door 6 en komen ze op 1 uit.
Anderen lezen de som als (6 ÷ 2) x (1 + 2). Ze lossen eerst de haakjes op tot 3, delen 6 door 2 tot 3, en vermenigvuldigen daarna 3 met 3, wat 9 geeft.
Het verschil zit hem in de volgorde waarin je de delen en vermenigvuldigingen uitvoert. Sommige mensen denken dat haakjes altijd voorrang krijgen, terwijl anderen alles strikt van links naar rechts oplossen als er geen extra haakjes zijn.
Het is precies die verwarring die dit soort raadsels zo interessant maakt. Iedereen heeft zijn eigen interpretatie, en daardoor lijkt het alsof beide antwoorden logisch zijn.
Emma, 34, kwam in een soortgelijke discussie terecht op het werk. “We zaten in de lunchpauze en iemand gooide dit raadsel op tafel,” vertelt ze. “Het begon als een grap, maar binnen een paar minuten stonden we met z’n allen rond het whiteboard te discussiëren. De helft zei 1, de andere helft zei 9.
Niemand wilde toegeven dat ze fout zaten.” Uiteindelijk moest Emma een wiskundige vriend bellen om duidelijkheid te krijgen. “Zelfs hij zei dat het afhing van hoe je de volgorde las. Dat maakte het alleen maar verwarrender.”
En dan is er nog de rol van technologie. Probeer deze som maar eens in verschillende rekenmachines in te voeren. Sommige geven 1, terwijl anderen 9 laten zien. Zelfs computersystemen lijken niet altijd op dezelfde manier met dit soort bewerkingen om te gaan.
Het laat zien hoe belangrijk het is om goed te begrijpen wat je doet, in plaats van blind op technologie te vertrouwen.
Maar goed, je hebt lang genoeg gewacht. Tijd voor het antwoord. Eerst los je de haakjes op: (1 + 2) = 3. Daarna kijk je naar de rest van de som: 6 ÷ 2 (3). Hier wordt het tricky.
Volgens de moderne interpretatie lees je dit als (6 ÷ 2) x 3, wat betekent dat je eerst 6 deelt door 2, wat 3 is, en dat vervolgens vermenigvuldigt met 3. De uitkomst is dus 9.
Maar voor degenen die de som anders interpreteerden en uitkwamen op 1: je bent niet alleen! Dit soort raadsels gaat vaak meer over hoe we denken dan over het juiste antwoord.
Het belangrijkste is dat het je aan het denken zet en dat je de volgende keer nét iets scherper kijkt voordat je een antwoord geeft. Want zeg nou zelf: hoe vaak hebben simpele sommen je zo aan het twijfelen gebracht?






