Een ogenschijnlijk eenvoudige rekensom, maar vaak eentje die een verrassing in petto heeft: 50 + 10 x 0 + 7 + 2 = ? Het lijkt op het eerste gezicht geen ingewikkelde som; het is gewoon optellen en vermenigvuldigen, toch? Toch blijkt dat veel mensen snel misgrijpen bij het oplossen van deze soort sommen.
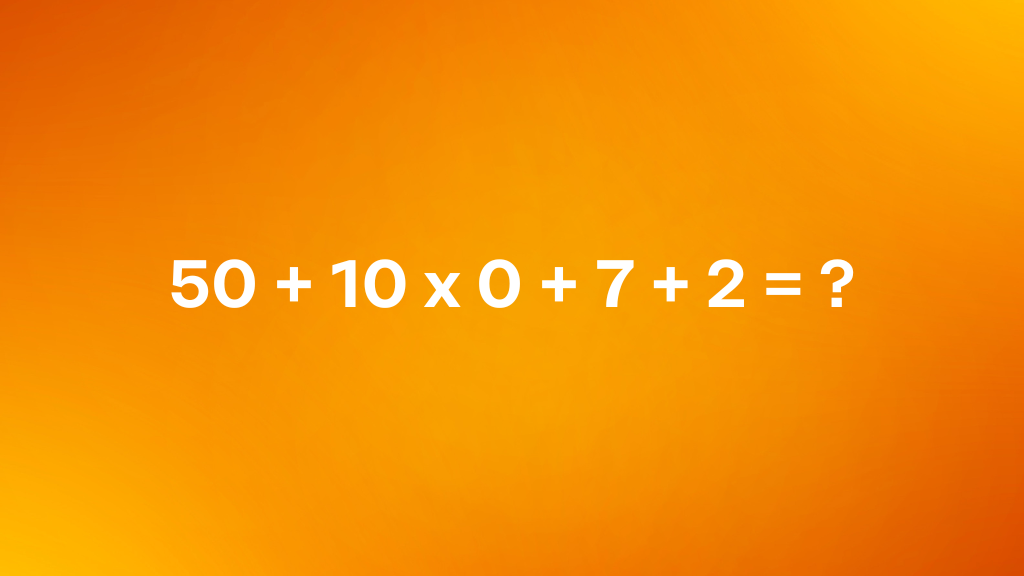
Hoe kan dat? Vaak heeft het te maken met hoe onze hersenen getraind zijn om simpele rekensommen snel op te lossen, waarbij we soms niet meer precies op de volgorde van de rekenregels letten.
Zodra een som ons een aantal eenvoudige getallen en tekens voorschotelt, willen we vaak haastig de bewerkingen uitvoeren in de volgorde waarin ze verschijnen. Maar is dat wel de juiste aanpak?
Bij rekensommen zoals deze wordt ons vooral getest op ons begrip van de rekenvolgorde. Je hebt vast wel eens gehoord van de basisrekenregels zoals ‘vermenigvuldigen voor optellen’ – een regel die vaak over het hoofd wordt gezien bij eenvoudige opgaven.
Deze regel bepaalt namelijk de volgorde waarin je rekent, ook wel de volgorde van bewerkingen genoemd.
In deze specifieke som worden verschillende getallen gecombineerd met zowel een vermenigvuldiging als een optelling. Het is dus niet zomaar een kwestie van links naar rechts de som oplossen.
Rekenregels dicteren namelijk dat vermenigvuldigen altijd voorrang heeft op optellen. Maar wat betekent dat precies voor ons antwoord?
Laten we de som eens stap voor stap bekijken om te zien hoe deze rekenregels ons helpen om het juiste antwoord te vinden.
Stap voor stap oplossen
De som begint met 50 + 10 x 0 + 7 + 2. De volgorde waarin we de bewerkingen moeten uitvoeren, is als volgt:
- Vermenigvuldigen gaat altijd voor optellen. In deze som betekent dit dat we beginnen met het deel dat we kunnen vermenigvuldigen: 10 x 0.
Wanneer we 10 x 0 uitrekenen, komen we uit op 0.
- Nu vervangen we 10 x 0 in de som door 0, zodat de som eruitziet als 50 + 0 + 7 + 2. Door de vermenigvuldiging als eerste te doen, vereenvoudigen we de som aanzienlijk.
- Nu resteert ons alleen nog de optelling: 50 + 0 + 7 + 2.
- We rekenen de optelling nu van links naar rechts uit:
- 50 + 0 geeft ons 50.
- 50 + 7 geeft ons 57.
- 57 + 2 brengt ons naar het uiteindelijke antwoord.
Het eindresultaat
Na alle stappen uitgevoerd te hebben, komen we uit op een eindantwoord. En dit is waar de grap van dit raadsel echt naar voren komt: het antwoord is namelijk 59.
Veel mensen zullen misschien snel antwoorden met een ander getal, zoals 69, doordat ze onbewust de 10 x 0 over het hoofd zien en toch alle getallen in de som blijven optellen.
Het is een klassieke fout die voorkomt wanneer we de regels van vermenigvuldigen vóór optellen even vergeten. Dat geeft een leuke wending aan wat aanvankelijk een eenvoudige som lijkt te zijn.
Waarom raken we in de war?
Waarom deze simpele regels ons soms parten spelen, heeft vaak te maken met de snelheid waarmee we simpele sommen willen oplossen. Wanneer een reeks getallen en bewerkingen ons brein overspoelt, neigen we naar het snelle, lineaire denken – van links naar rechts – zonder te pauzeren bij de rekenregels.
Onze hersenen verwerken de som als een enkele lijn van getallen en plussen, maar de werkelijke volgorde van bewerkingen eist soms iets anders.
Deze hersenkraker leert ons dat wiskunderegels altijd de structuur van het antwoord bepalen. Het is een leuke manier om jezelf eraan te herinneren om niet zomaar door getallen te vliegen zonder eerst goed naar de tekens en volgorde te kijken.
Wat we hieruit kunnen leren
Sommen zoals deze zijn een goede oefening in concentratie en nauwkeurigheid. Ze laten zien hoe snel we geneigd zijn om over eenvoudige, maar belangrijke regels heen te stappen. Het is een perfecte test voor ons vermogen om aandachtig te blijven bij ogenschijnlijk simpele vraagstukken.
Dus, wanneer je de volgende keer een som als 50 + 10 x 0 + 7 + 2 ziet, neem even een moment om na te denken over de volgorde van bewerkingen. Want zoals we hier hebben geleerd, kan die ene kleine stap het verschil maken tussen een goed of fout antwoord.





