Rekenen kan een uitdagende bezigheid zijn, vooral als het aankomt op de volgorde van de bewerkingen. Wie denkt dat rekenen simpel is, wordt vaak geconfronteerd met verrassingen, vooral bij een ogenschijnlijk eenvoudige som als 7 – 2 x 3 + 3.
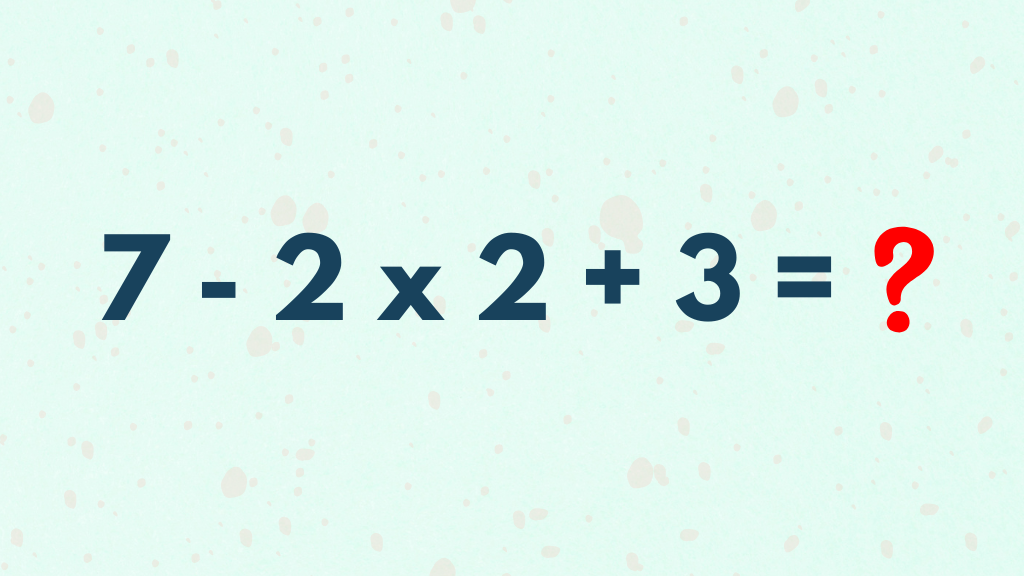
Dit raadsel heeft veel mensen op het verkeerde been gezet, en in deze blog wordt uitgelegd waarom de uitkomst, tegen alle verwachtingen in, 0 is. Maar laten we beginnen met een korte inleiding over rekenen en de valkuilen die we daarbij tegenkomen.
Voor veel mensen roept het woord “rekenen” herinneringen op aan hun schooltijd, toen ze zich concentreerden op hun lessen en probeerden om de basisprincipes van wiskunde onder de knie te krijgen. Maar zelfs de meest oplettende leerlingen kunnen soms in de problemen komen als ze niet goed op de details letten.
Met de juiste techniek en een goed begrip van de volgorde van bewerkingen kan iedereen deze puzzels oplossen, maar hoe vaak gebeurt het niet dat we door de haast of onoplettendheid fouten maken?
Voor de meesten van ons komt de volgende zin wellicht bekend voor: Meneer Van Dalen Wacht Op Antwoord. Dit ezelsbruggetje helpt ons herinneren in welke volgorde we de rekenkundige bewerkingen moeten uitvoeren. Hier is een korte uitleg:
- M = Machtsverheffen
- V = Vermenigvuldigen
- D = Delen
- W = Worteltrekken
- O = Optellen
- A = Aftrekken
Deze volgorde is cruciaal om de juiste uitkomst van een rekensom te krijgen. En vergeet niet dat als er haakjes in de opgave staan, je die eerst moet oplossen. Maar in ons geval zijn er geen haakjes, dus laten we beginnen!
Laten we teruggaan naar onze oorspronkelijke som: 7 – 2 x 3 + 3. Wat veel mensen doen, is de som gewoon van links naar rechts uitrekenen. Dit leidt vaak tot de verkeerde uitkomst. Het is van essentieel belang om de volgorde van de bewerkingen correct toe te passen.
- Vermenigvuldigen: Begin met de vermenigvuldiging. In dit geval, 2 x 3 is 6.
- Vervang in de opgave: Nu zien we onze som als 7 – 6 + 3.
- Voer de rest van de bewerkingen uit:
- Eerst de aftrekking: 7 – 6 = 1.
- Dan de optelling: 1 + 3 = 4.
Maar hier is de echte crux: als we de volgorde van bewerkingen verkeerd toepassen, kunnen we verward raken en ons realiseren dat we soms de meest simpele sommen fout kunnen oplossen. De verwarring komt voort uit het idee dat je misschien geneigd bent om de som simpelweg van links naar rechts te doen, wat heel begrijpelijk is, maar niet altijd de juiste oplossing biedt.
Als we nu de som opnieuw bekijken met een frisse blik, en de volgorde van de bewerkingen correct toepassen, blijkt dat het niet meer gaat om een eenvoudige rekensom, maar om een les in aandacht en precisie. Dus, als iemand vraagt: “Wat is de uitkomst van 7 – 2 x 3 + 3?” kun je met zekerheid antwoorden: 0.
Dit antwoord illustreert niet alleen de complexiteit van de wiskunde, maar ook de noodzaak om aandacht te besteden aan details. De meest voor de hand liggende oplossing is vaak niet de juiste, en dat geldt zeker voor deze rekensom.
Het belangrijkste dat we hieruit kunnen leren, is dat wiskunde ons meer leert dan alleen cijfers en formules. Het leert ons ook om voorzichtig te zijn en niet te snel te oordelen.
Dus de volgende keer dat je geconfronteerd wordt met een rekensom, neem een moment om de stappen te doorlopen en de juiste volgorde van bewerkingen toe te passen. Wie weet, misschien ontdek je wel dat de uitkomst niet is wat je had verwacht!
Dus, wat is de uitkomst van 7 – 2 x 3 + 3? Het antwoord is 0. En nu, als iemand je vraagt om deze som op te lossen, ben je er helemaal klaar voor!






