Een ogenschijnlijk simpele rekensom heeft opnieuw voor flink wat ophef gezorgd op het internet. De oorzaak? Een eenvoudige vergelijking: 8 ÷ 2(2 + 2). Op het eerste gezicht lijkt het een standaard wiskundeprobleem, maar miljoenen mensen bleken het toch niet eens over het juiste antwoord. De som werd viraal nadat een tweet uit 2019 dit als een soort hersenkraker presenteerde, en sindsdien laait de discussie telkens weer op.
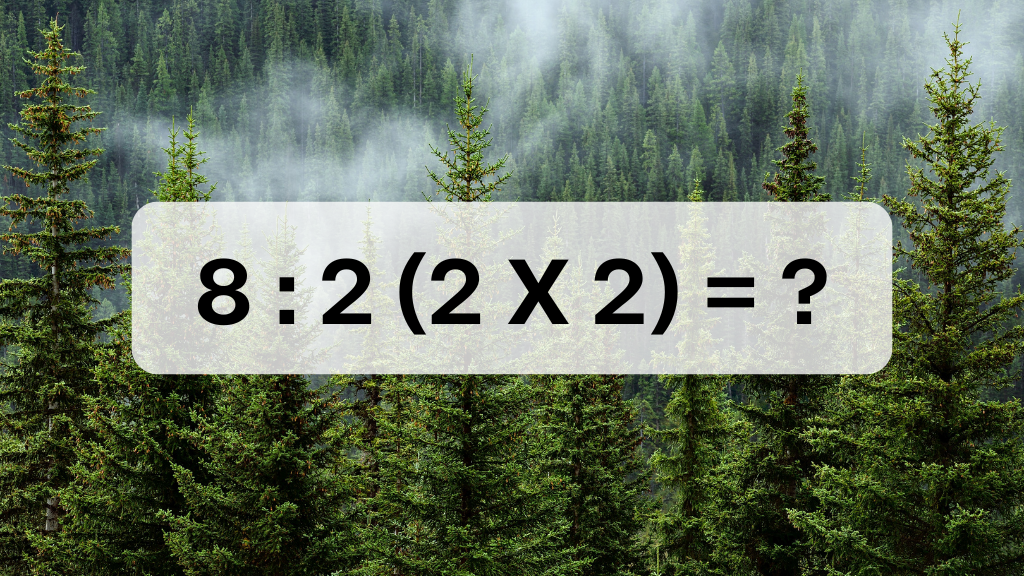
Wat maakt deze rekensom nou zo bijzonder? Het antwoord lijkt afhankelijk van hoe je de volgorde van bewerkingen toepast – en daar verschillen de meningen behoorlijk over.
De klassieke wiskunderegel: volgorde van bewerkingen
Iedereen die ooit wiskunde op school heeft gehad, kent de standaardregels: eerst haakjes oplossen, dan machten en wortels, gevolgd door vermenigvuldigen en delen van links naar rechts, en tot slot optellen en aftrekken.
Dit wordt in het Nederlands ook wel afgekort als HMDOMA (Haakjes, Machten, Delen, Optellen, Min, Aftrekken) of internationaal als PEMDAS of BODMAS.
Als deze regels netjes worden gevolgd, ziet de som er zo uit:
8 ÷ 2(2 + 2)
→ 8 ÷ 2(4)
→ 8 ÷ 2 × 4
Daar komt de crux: de deling en vermenigvuldiging komen nu ná elkaar. En volgens de conventie moeten die dan van links naar rechts worden opgelost, dus:
8 ÷ 2 = 4
4 × 4 = 16
Volgens deze redenering is het antwoord dus 16. En dat is ook wat de meeste rekenmachines geven als de som precies zo wordt ingevoerd.
Waarom veel mensen toch 1 antwoorden
Toch zijn er mensen – ook onder wiskundigen – die pleiten voor een andere interpretatie. Zij zeggen dat 2(4) gezien moet worden als één geheel, dus als een impliciete vermenigvuldiging die voorrang krijgt boven deling.
Volgens deze redenering:
8 ÷ 2(4) = 8 ÷ (2 × 4) = 8 ÷ 8 = 1
Deze redenering leunt op het idee dat wanneer vermenigvuldiging direct naast een haakje staat, dit een andere prioriteit heeft dan gewone vermenigvuldiging of deling.
Vooral in oude wiskundeboeken of bij handmatig schrijven van formules is dit een manier van noteren die voor verwarring kan zorgen.
Rekenmachines en software zijn het ook niet altijd eens
Het interessante aan dit probleem is dat zelfs sommige rekenmachines en software verschillende antwoorden geven, afhankelijk van hoe de formule precies wordt ingevoerd.
Een grafische rekenmachine of een programmeertaal als Python zal mogelijk 16 geven, terwijl bepaalde spreadsheetprogramma’s of online calculators onder specifieke instellingen 1 als uitkomst laten zien.
Dit maakt duidelijk hoe belangrijk haakjes zijn bij het correct interpreteren van een formule. Want uiteindelijk draait het hier niet alleen om de rekensom zelf, maar om hoe die geschreven is.
Waarom deze discussie blijft boeien
Wat deze wiskundesom zo fascinerend maakt, is dat het laat zien hoe taal en logica kunnen botsen. Het probleem zit hem namelijk niet zozeer in de wiskundige regels zelf, maar in hoe mensen ze interpreteren.
In een goed geschreven formule zou er meer duidelijkheid zijn: bijvoorbeeld door extra haakjes te gebruiken om aan te geven wat nu precies eerst moet.
Het is een perfect voorbeeld van hoe kleine details een groot verschil kunnen maken. Niet voor niets wordt dit soort rekensommen vaak gebruikt in toelatingstesten of IQ-tests, juist omdat ze laten zien wie er secuur werkt – en wie vertrouwt op intuïtie.
Wat kunnen we ervan leren?
Deze simpele som leert ons vooral dat duidelijke communicatie cruciaal is – ook in wiskunde. Wil je dat iedereen hetzelfde antwoord krijgt?
Dan moet je de som ook zo opschrijven dat er geen ruimte is voor meerdere interpretaties.
En voor wie zich afvraagt welk antwoord nou écht goed is: de meeste moderne wiskundigen en onderwijsinstellingen geven 16 als het juiste antwoord, op basis van de standaard volgorde van bewerkingen.
Maar dat sluit niet uit dat de andere redenering begrijpelijk is – zolang het probleem niet beter is gedefinieerd.
Eén ding staat vast: als zelfs een som met maar drie getallen en wat haakjes het internet kan ontploffen, dan is wiskunde allesbehalve saai.






