Veel mensen hebben moeite met de volgorde van bewerkingen in wiskunde, ook wel bekend als de rekenregels. Deze regels zijn cruciaal om correct tot een antwoord te komen, vooral wanneer er meerdere bewerkingen in één formule staan, zoals optellen, aftrekken, vermenigvuldigen, en delen. Een eenvoudige fout in de volgorde van bewerkingen kan al snel tot een verkeerd antwoord leiden, zelfs als de som simpel lijkt. In dit artikel behandelen we een voorbeeld dat vaak misgaat: de berekening van de som 18 ÷ 3 (5 – 4 + 1).
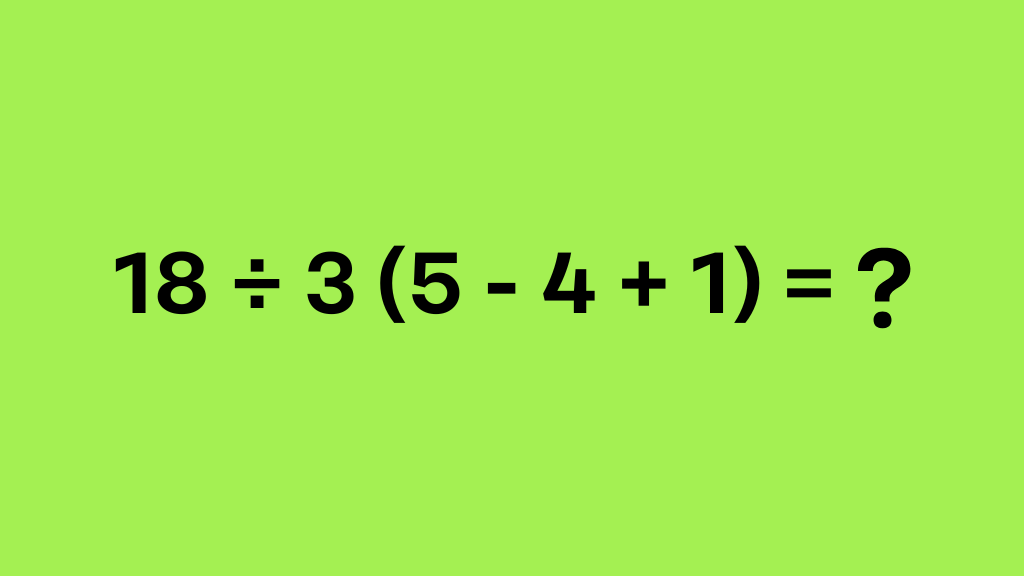
Deze som lijkt op het eerste gezicht eenvoudig, maar als we de rekenregels niet correct toepassen, komen we bij een ander antwoord uit dan bedoeld. In dit artikel gaan we stap voor stap door de berekening heen en leggen we uit waarom de rekenregels zo belangrijk zijn. Onderaan geven we het juiste antwoord op de som en een uitleg waarom dit het juiste antwoord is. Dit artikel is nuttig voor studenten, ouders en iedereen die zich afvraagt waarom de volgorde van bewerkingen er zo toe doet in wiskunde.
Wat zijn de rekenregels?
De volgorde van bewerkingen in wiskunde wordt vaak aangegeven door het acroniem DMVAO:
- Delen en vermenigvuldigen: deze bewerkingen gaan voor optellen en aftrekken en worden van links naar rechts uitgevoerd.
- Machtsverheffen en worteltrekken: deze bewerkingen gaan vóór delen en vermenigvuldigen.
- Afronden met optellen en aftrekken: deze bewerkingen komen pas aan het einde.
Maar voor het oplossen van sommen zoals 18 ÷ 3 (5 – 4 + 1), moeten we ook onthouden dat haakjes altijd als eerste worden uitgerekend. Laten we stap voor stap door de som heen gaan om te zien hoe we tot het antwoord komen.
Stap 1: Werk de haakjes uit
De som die we gaan uitrekenen is: 18 ÷ 3 (5 – 4 + 1).
Volgens de rekenregels moeten we altijd eerst de bewerkingen binnen haakjes uitwerken. In deze som staat er 5 – 4 + 1 binnen de haakjes. We beginnen dus met:
- 5 – 4 = 1
- 1 + 1 = 2
De som wordt nu eenvoudiger en ziet er zo uit:
18 ÷ 3 × 2
Door de haakjes als eerste uit te werken, hebben we nu alleen nog een deling en een vermenigvuldiging over.
Stap 2: Delen en vermenigvuldigen van links naar rechts
Nu we de haakjes hebben uitgewerkt, moeten we bepalen wat de volgende stap is. Volgens de rekenregels gaan delen en vermenigvuldigen vóór optellen en aftrekken. En in dit geval is het belangrijk om delen en vermenigvuldigen van links naar rechts toe te passen. Dit betekent dat we eerst 18 ÷ 3 uitwerken voordat we gaan vermenigvuldigen.
- 18 ÷ 3 = 6
Nu hebben we de som vereenvoudigd tot:
6 × 2
Laten we nu de laatste stap uitvoeren.
Stap 3: Vermenigvuldigen
Nu hebben we alleen nog maar 6 × 2 over. Dit levert ons het uiteindelijke antwoord:
- 6 × 2 = 12
Dus, door de rekenregels correct toe te passen, komen we uit bij het antwoord:
18 ÷ 3 (5 – 4 + 1) = 12
Veel mensen komen echter bij een ander antwoord uit, meestal door de volgorde van bewerkingen niet correct toe te passen. Een veelgemaakte fout is om de vermenigvuldiging direct na de haakjes uit te voeren, zonder eerst de deling af te werken. Dit leidt tot een foutief antwoord. Het juiste antwoord is echter 12, zoals we stap voor stap hebben uitgewerkt.
Rekenregels helpen ons om duidelijk en gestructureerd te werken met wiskundige bewerkingen. Door altijd dezelfde regels te volgen, voorkomen we fouten en komen we consistent tot de juiste antwoorden. Dit is niet alleen nuttig voor het oplossen van sommen zoals 18 ÷ 3 (5 – 4 + 1), maar voor elke complexe berekening. Vooral bij het werken met formules en algebraïsche vergelijkingen zijn de rekenregels essentieel om fouten te vermijden.
De volgorde van bewerkingen vormt de basis voor vele andere onderdelen van de wiskunde. Zodra je deze regels begrijpt en correct kunt toepassen, worden veel wiskundige problemen een stuk eenvoudiger en kun je met meer vertrouwen rekenen.
Conclusie
De som 18 ÷ 3 (5 – 4 + 1) is een uitstekend voorbeeld van waarom het correct toepassen van de rekenregels zo belangrijk is. Door eerst de haakjes uit te werken, daarna delen en vermenigvuldigen van links naar rechts uit te voeren, komen we bij het juiste antwoord van 12. Als je deze volgorde van bewerkingen goed onthoudt en steeds toepast, kun je de meeste wiskundige problemen met succes oplossen.
Dus de volgende keer dat je een berekening zoals deze tegenkomt, weet je precies hoe je stap voor stap te werk moet gaan.






