Wiskundige vaardigheden zijn niet alleen van belang in de schoolbanken, maar spelen ook een cruciale rol in het dagelijks leven. Of het nu gaat om het berekenen van fooien in restaurants, het bepalen van kortingspercentages tijdens uitverkoop of zelfs het budgetteren van huishoudelijke uitgaven, een goed begrip van basisrekenvaardigheden is essentieel.
Het oefenen van deze vaardigheden stelt mensen in staat om snel en nauwkeurig problemen op te lossen die zich in allerlei situaties kunnen voordoen. Een interessant voorbeeld hiervan is de uitdaging om een moeilijke vergelijking op te lossen.
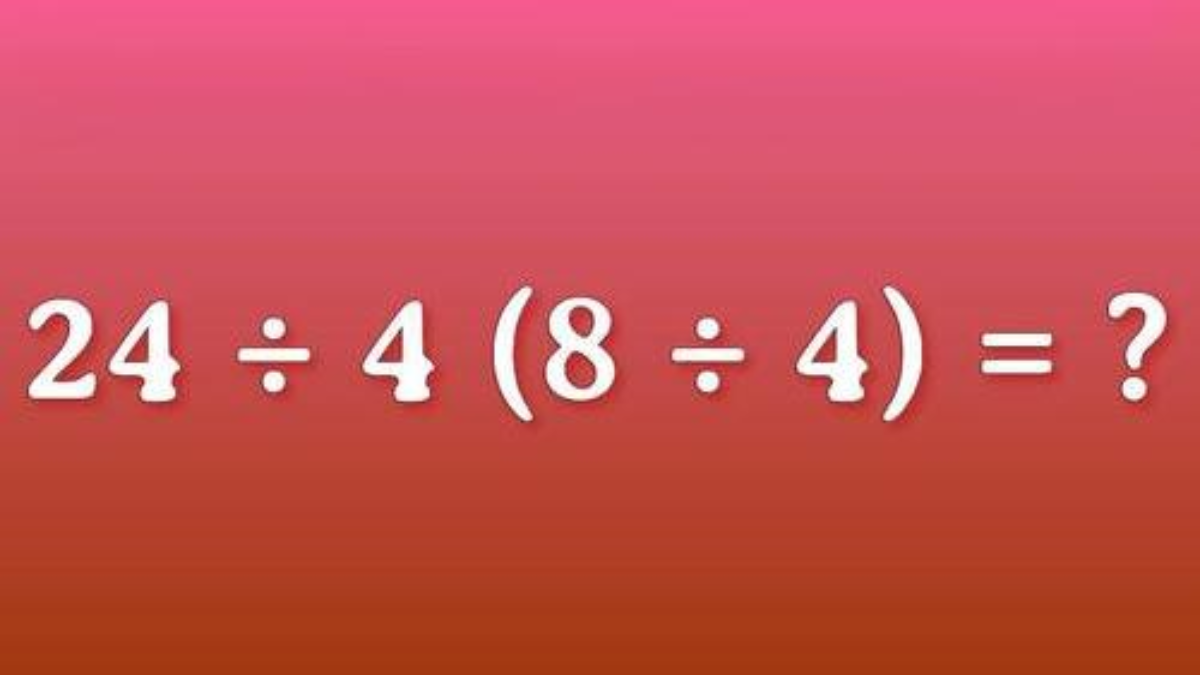
Het vraagstuk begint met een eenvoudige opdracht: los de volgende vergelijking op en bepaal of het antwoord 3 of 12 is.
De vergelijking luidt: 24 ÷ 4 × ( 8 ÷ 4 )
Om dit op te lossen, moeten we de regel van PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)) toepassen, wat de volgorde van bewerkingen aangeeft. Allereerst behandelen we de haakjes: 8 ÷ 4 geeft als resultaat 2.
Vervolgens gaan we verder met de rest van de vergelijking. We hebben 24 ÷ 4 wat gelijk is aan 6. Nu vermenigvuldigen we deze twee resultaten: 6 × 2 = 12. Daar hebben we het antwoord: 12.
Dit toont aan hoe belangrijk het is om de volgorde van bewerkingen correct toe te passen om tot het juiste antwoord te komen. Dit principe is niet alleen relevant voor wiskunde op school, maar speelt een cruciale rol in het dagelijks oplossen van problemen en het maken van beslissingen op basis van nauwkeurige berekeningen. Door regelmatig te oefenen met dit soort vraagstukken blijven wiskundevaardigheden scherp en kunnen ze effectief worden toegepast in diverse praktische situaties. Het bevordert niet alleen het vermogen om snel problemen op te lossen, maar versterkt ook het vertrouwen in het omgaan met numerieke uitdagingen in het alledaagse leven.






